このページでは、数独(ナンバープレイス)を解く基本的な方法について解説しています。 しっかり読んでマスターすれば、大抵の問題は解くことができるようになるでしょう。
なお、解説に出てくる用語を簡単に定義しておきたいと思います。
数独を解くテクニック
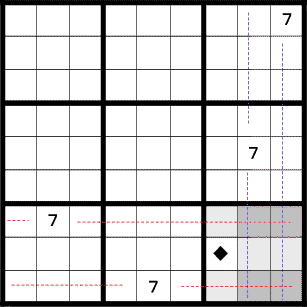
右下の3×3のブロック(エリア)を見て下さい。 エリアの横を見てみると、7が2つあります。 7は上の行と下の行にあるので、 右下のエリアには真ん中の行に7が入ることが分かります。
今度は縦を見てみると、やはり7が2つあります。 真ん中の列と右の列にあるので、 考慮中のエリアでは左の列に入ることが分かります。
以上を総合すると、♦のマスに7が入ることが分かります。
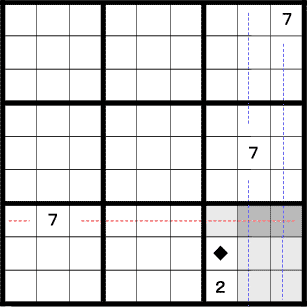
上と似ていますが、今度は横のエリアに7が1つしかありません。
しかし、同じようにして7が入らないマスを潰していきます。左列の真ん中と下が残ります。
下側には既に別の数字が入っているので、♦の位置に7が入ることになります。
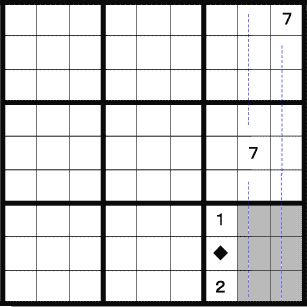
この場合は、横に7がありません。 しかし縦には7が2つあるので、一番下のエリアには左の列に7が入ることが分かります。
エリアの左の列には既に2つの数字が入っています。 従って残る1マスに7が入ることになります。
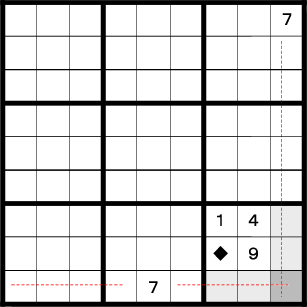
この場合は横にも縦にも7が1つしかありません。 従って右下のエリアで7が入らない部分を潰していくと図のようになります。
残った4マスのうち3つは既に数字が入っています。 ですから♦のマスに7が入ることになります。
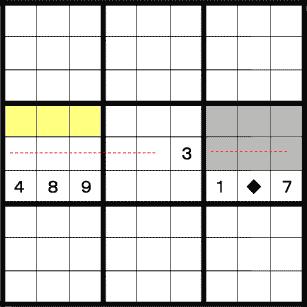
上図はよく中盤に出てくるケースです。中央エリアの真ん中の行には3があります。 従ってその両脇のエリアの真ん中の行に3は入りません。
次に左のエリアを見ます。すると一番下の行は既に数字が埋まっています。 この結果3が入るのは上の行のどこか(黄色のマス)ということになります。
以上より、右のエリアでは一番下の行に3が入ります。 既に2つのマスが埋まっているので、♦の位置に3が入ります。
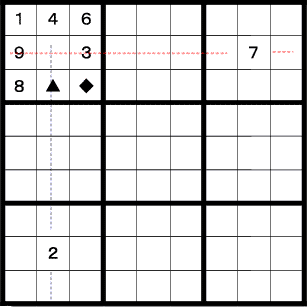
今度は終盤に出てくる定石です。左上のエリアのように沢山埋まったエリアがあれば、 それを全部埋めることができないか調べます。残りの数字が2,5,7であることを確認します。
上図は、真ん中の列に2が入らないことが分かります。ということで残っているのは♦のマスだけです。 そこに2が入ります。
そうすると、残り2つのマスのうち▲の所に7が入ります。
最後に残ったマスは、残りの数字すなわち5が入ることになります。
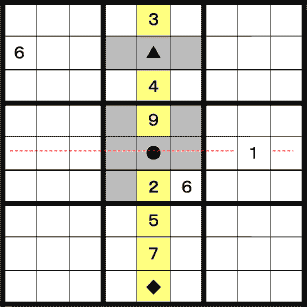
中央の列をご覧下さい。残りの数字を調べてみると、1,6,8であることが分かります。
このうち、灰色で塗りつぶした部分に6は入らないことが分かります。 従って♦のマスに6が入ります。残りは1と8です。
真ん中のエリアの●のマスには1が入らないことが分かります。 従って▲に1、●に8が入ります。
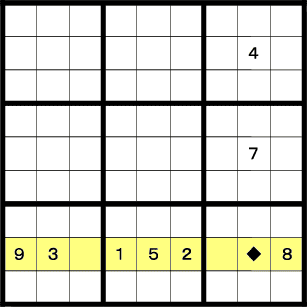
下から2段目の黄色の行を見てみましょう。残りの数字は4,6,7です。
♦のマスの縦列を見てみると、4と7があります。 従ってこのマスには残りの数字である6が入ることになります。
空マスが残り少なくなった場合は、1つ前の図のように特定の数字に注目する方法と、 今回のように特定のマスに注目する2通りの方法によって埋めていきます。
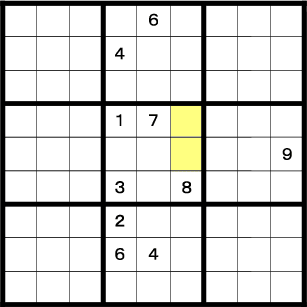
よく使用する比較的高度な定石を紹介します。
中央のエリアをご覧下さい。4は黄色のマスにしか入らないことが分かるでしょう。 6も同様です。
現時点でどちらが4でどちらが6かは分かりません。 しかしこの2マスに4と6が入ることは確定しています。 他の数字は入りません←ここがポイントです。
中央エリアの残る部分は3マスだけで、 そこに入る数字は2,5,9です。 右エリアに9、下のエリアに2があるので、それらの数字が確定することがお分かりかと思います。
3つのマスを3つの数字が占めることもありますが、それは次の図で確認してみましょう。
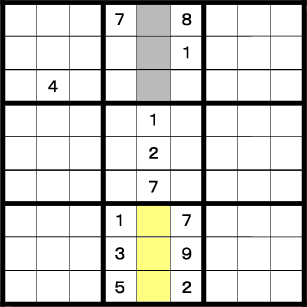
真ん中の3つのエリア群を見てみましょう。
一番下のエリアの黄色い3マスは、4,6,8の何れかの数字が入ります。 従って一番上のエリアの灰色の3マスは、3,5,9が入ります。 3つのマスは3つの数字が占拠しました。
一番上のエリアの残り3マス(白い空きマス)は2,4,6が入ります。 左のエリアに4があるので、4→2→6の順番で数字が埋まることが分かるでしょう。
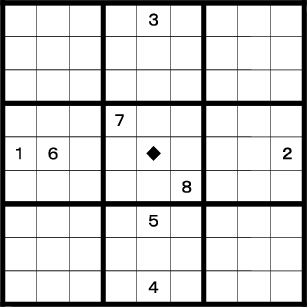
今度は盤面を広く見て解く定石を紹介してみます。
♦の部分は9が確定しています。列・行・自身のエリア内を見てみると、 1~8までの数字があることが分かります。
特定の1マスを盤面全体を見て決定する、比較的高度な定石と言えます。
実際には3つ前の法則と一緒です。 しかし列や行がそんなに埋まっていなくても確定していることがあるので、 行き詰った時には調べてみる価値のある方法です。

最後に、ちょっと難しい仮置きの法則について説明しておきます。 完全に手詰まりになった場合、入る数字が絞られたマスに数字を仮置きして、 矛盾がないか調べることにより解決できる場合があります。
左上のエリアの黄色いマスには、3か9が入ります。 仮に3を入れてみましょう。 そうすると、右上→右下→左下のエリアの灰色のマスに3が入っていきます。 しかし左から2列目は3が2つになってしまいました。 矛盾が生じたので、黄色のマスは3ではなく9が正解となります。